Skip to main content

集合

info

大部分都学过，记一些需要注意的地方。

集合的关系​

相等：A=B  ⟺  A⊆B∧B⊆A  ⟺  ∀x(x∈A↔x∈B)A=B\iff A \subseteq B\wedge B\subseteq A \iff \forall x(x \in A\leftrightarrow x \in B)

真包含：A⊂B  ⟺  A⊆B∧A≠B  ⟺  ∀x(x∈A→x∈B)∧∃x(x∈B∧x∉A)A\subset B\iff A \subseteq B\wedge A\neq B\iff \forall x(x\in A\to x\in B)\wedge \exists x(x\in B \wedge x \notin A)

全集 可以写为一个永真式，空集 可以写为一个矛盾式。

info

若 A⊆BA\subseteq B，证明 A∩B=AA\cap B=A.

A∩B  ⟺  ∀x(x∈A∩B↔x∈A)  ⟺  ∀x((x∉A∩B∨x∈A)∧(x∉A∨x∈A∩B))  ⟺  ⋯  ⟺  ∀x(x∈A→x∈B)  ⟺  A⊆B\begin{aligned} &A\cap B\\ \iff&\forall x(x \in A\cap B\leftrightarrow x\in A)\\ \iff&\forall x((x\notin A\cap B\vee x\in A)\wedge (x\notin A \vee x\in A\cap B))\\ \iff&\cdots\\\iff&\forall x(x\in A\to x\in B)\\\iff&A\subseteq B \end{aligned}

容斥定理：见概率论。

二元关系​

tip

序偶 使用尖括号表示，和集合不同，其中元素是有序的，且只有两个元素，多元的被称为有序 nn 元组。

集合的笛卡尔积

设集合 A,BA,B，由集合 AA 的元素为第一元素，集合 BB 的元素为第二元素的全部 序偶 的 集合，称为 AA 和 BB 的笛卡尔积，记作 A×BA\times B；笛卡尔积不满足交换率和结合率，有 特例 A×∅=∅×B=∅A\times \emptyset=\emptyset\times B=\emptyset ；对交集和并集满足分配率，但相对顺序不变。

由乘法原理可得，笛卡尔积结果的元素个数为 ∣A∣×∣B∣|A|\times|B|；

若 C≠∅C\neq\emptyset ，则 A⊆B  ⟺  A×C⊆B×C  ⟺  C×A⊆C×BA\subseteq B\iff A\times C\subseteq B\times C\iff C\times A\subseteq C\times B；

若 A,B,C,DA,B,C,D 非空，则 A×B⊆C×D  ⟺  A⊆C∧B⊆DA\times B\subseteq C\times D\iff A\subseteq C\wedge B\subseteq D；

集合的重复运算可以简写为次方形式 A×A×A=A3A\times A\times A=A^3，多个集合的笛卡尔积实际上是全排序，结果中的每个元素都是一个有序 nn 元组 <a,b,c><a,b,c>，而不是序偶中包含序偶 <<a,b>,c><<a,b>,c>；

关系​

笛卡尔积的子集，描述元素之间的某种对应关系；关系可以表述为 <x,y>∈R  ⟺  xRy<x,y>\in R\iff xRy，称之为 xx 和 yy 有 RR 关系。

关系的定义域：对于二元关系，<x,y>∈R<x,y>\in R 的第一个元素组成的集合，就是 RR 的定义域，记作 dom(R)={x∣∃y(<x,y>∈R)}dom(R)=\left\{x|\exists y(<x,y>\in R)\right\}

关系的值域：对于二元关系，<x,y>∈R<x,y>\in R 的第二个元素组成的集合，就是 RR 的值域，记作 ran(R)={y∣∃x(<x,y>∈R)}ran(R)=\left\{y|\exists x(<x,y>\in R)\right\}

空关系是一个空集；完全关系 就是笛卡尔积本身；恒等关系：IA∈A×AI_{A}\in A\times A，且 IA={<x,x>∣x∈A}I_{A}=\{<x,x>|x\in A\}，关系矩阵是一个对角矩阵；

关系的性质​

tip

本节以及后续小节内容都是 R∈A×AR\in A\times A，即从 AA 到 AA 的关系。

自反性：对于 ∀x∈A\forall x \in A，都有 <x,x>∈R<x,x>\in R，则称其为 自反关系；例如 x≤xx\leq x 就是自反关系；自反关系的有向图 每个节点 都有环，并且主对角线都为 1；

反自反性：将自反性的属于改为不属于，如 x<xx<x 就是反自反关系，每个节点都无环，主对角线都为 0；

对称性：∀x∀y((x∈A∧y∈A∧xRy)→yRx)\forall x\forall y((x\in A\wedge y\in A\wedge xRy)\to yRx)，即若有 xRyxRy 则必有 yRxyRx，例如人群中的邻居关系和朋友关系就是对称关系；关系图中两个不同的节点若有边，则有方向相反的两条边；关系矩阵为对称矩阵；

反对称性：如果有 xRyxRy 和 yRxyRx，则 x=yx=y，如 ≤\leq 就是反对称关系，关系图中两个不同的节点最多有一条边，关系矩阵中以主对角线对称的两个元素中最多有一个 1；

传递性：若有 xRy，yRzxRy，yRz，则一定有 xRzxRz，例如 ≤,<,⊂,⊆\leq,<,\subset,\subseteq 都是传递关系；关系图和关系矩阵无特征；

caution

传递性定义的谓词公式形式的前件为假时，传递性同样成立，即若 xRy,yRzxRy,yRz 中至少一个为假，仍然传递。

因此独立无环或无环的节点不影响传递，空关系、恒等关系和完全关系都是传递的。

复合运算​

RR 是从 XX 到 YY 的关系，SS 是从 YY 到 ZZ 的关系，则 RR 和 SS 的复合关系是从 XX 到 ZZ 的关系，记作 R∙SR\bullet S（空心）

不满足交换率，但是满足结合率和分配率：

  1. R∙(S∪T)=(R∙S)∪(R∙T)R\bullet (S\cup T)=(R\bullet S)\cup(R\bullet T)
  2. R∙(S∩T)⊆(R∙S)∩(R∙T)R\bullet(S\cap T)\subseteq(R\bullet S)\cap(R\bullet T)

若 RR 是 AA 到 BB 的关系，II 为恒等关系，则 R∙IB=IA∙R=RR\bullet I_{B}=I_{A}\bullet R=R；

关系的复合也可以写为乘幂的形式 R∙R∙R=R3R\bullet R\bullet R=R^3，特别定义 R0=IAR^0=I_{A}；

求逆运算：将关系中的所有序偶的两个元素位置互换，记作 RCR^C 或 R−1R^{-1}；关系图中所有有向线段方向颠倒；关系矩阵转置；

(R∪S)−1=R−1∪S−1(R∩S)−1=R−1∩S−1(R−S)−1=R−1−S−1R⊆S=R−1⊆S(R∙S)−1=S−1∙R−1\begin{aligned} (R\cup S)^{-1}=R^{-1}\cup S^{-1}\\(R\cap S)^{-1}=R^{-1}\cap S^{-1}\\(R-S)^{-1}=R^{-1}-S^{-1}\\R\subseteq S=R^{-1}\subseteq S\\(R\bullet S)^{-1}=S^{-1}\bullet R^{-1} \end{aligned}

复合关系的逆要互换位置。

关系对称，当且仅当 R−1=RR^{-1}=R。

闭包运算​

通过关系复合和求逆运算构成的新关系，包括 自反闭包、对称闭包和传递闭包。

给定 AA 上的关系 R,R′R,R'

  1. R⊆R′R\subseteq R'
  2. R′R' 自反
  3. R′R' 是最小的，即对于任何 AA 上的自反关系 R′′R''， R⊆R′′  ⟹  R′⊆R′′R\subseteq R''\implies R'\subseteq R'' 则称其为自反闭包，记作 r(R)r(R)；

将上述定义修改为最小的对称关系和传递关系，则得到对称闭包和传递闭包，记作 s(R)s(R) 和 t(R)t(R)。

计算方法

  1. r(R)=R∪IAr(R)=R\cup I_{A}
  2. s(R)=R∪R−1s(R)=R\cup R^{-1}
  3. t(R)=R∪R2⋯∪Rn(n→∞)t(R)=R\cup R^2\cdots\cup R^n(n\to \infty)，看起来无法实现，实际上某项之后就是空集或者是之前出现过的，直接化简即可，因此有定理，若 ∣A∣=n|A|=n，则 t(R)=R∪R2⋯∪Rnt(R)=R\cup R^2\cdots\cup R^n

集合的划分与覆盖​

覆盖：AA 中的所有元素 AiA_{i} 都是一个集合，并且 A1∪⋯∪An=X,X≠∅A_{1}\cup\cdots\cup A_{n}=X,X\neq\emptyset，则称 AA 是 XX 的一个覆盖；

划分：若 AA 是 XX 的一个覆盖，并且 Ai∩Aj=∅A_{i}\cap A_{j}=\emptyset，则称 AA 是 XX 的一个划分；划分一定是覆盖；最小划分就是 XX 本身，最大划分是 XX 中的每一个元素；

交叉划分：若 A,BA,B 都是 XX 的一个划分，所有的 Ai∩BiA_{i}\cap B_{i} 组成的集合 CC，则称 CC 是 AA 与 BB 的交叉划分；

等价关系和等价类​

关系 RR 是自反、传递和对称的，则称 RR 是 AA 上的等价关系；

等价关系的关系图是由若干个独立 的子图构成，每个独立子图都是 完全关系图；

等价类，就是集合中与另一个元素 aa 满足等价关系的所有元素的集合，叫做 aa 的等价类；等价类的个数就是独立子图的个数，因此不同元素的等价类之间没有交集。

商集，所有等价类构成的是原集合的一个划分，该划分成为 商集，表示为 A/RA/R；

通过集合的一个划分，可以确定其等价关系 R=A12∪A22⋯R=A_{1}^2\cup A_{2}^2\cdots.

相容关系与相容类​

自反，对称，但是不传递，就是相容关系；每个结点都有环，不同结点之间可以无边，有边一定成对出现；对称矩阵，主对角线全是 1。

相容类，RR 是集合 AA 上的相容关系，C⊆XC\subseteq X，如果对于任意 <x,y>∈C<x,y>\in C ，都有 <x,y>∈R<x,y>\in R，则称 CC 是 RR 的一个相容类；这和等价类的定义不同，相容类之间可以互相包含，因此有概念 最大相容类，对应图中全相联的最大多边形；相容类之间也可以不包含，所有的最大相容类构成一个集合，成为 XX 的 完全覆盖。

偏序关系​

满足自反、反对称和传递的关系 RR，称 <A,R><A,R> 是 偏序集；实数集合上的 ≤,≥,⊆\leq,\geq,\subseteq 都是偏序关系。

哈斯图：

  1. 第一元素在左/下，第二元素在右/上；
  2. 由于存在传递性，如 a→b,b→c,a→ca\to b,b\to c,a\to c，则 a→ca\to c 可以省略不画；
  3. 自反，环不用画。

全序关系（线序、链），集合中的任意两个元素都满足 偏序关系（如 a→ba\to b 或者 b→ab\to a，不必全部满足），则成为全序关系，这样构成一条链，如 1≤2≤3≤4⋯1\leq 2\leq 3\leq 4\cdots

极大元，偏序关系中，是否存在这样的元素，若有一个元素与其形成偏序关系，那么这个元素只能是自己；

极小元，是否存在这样的元素，若有一个元素与其形成被偏序关系，那么这个元素只能是自己

caution

极大元和极小元应该在集合的子集中寻找，并且并不唯一，甚至可能为同一个元素。

最大元，是否存在一个元素，使得其他的元素都与其是偏序关系

最大元，是否存在一个元素，使得其他的元素都与其是被偏序关系

上界和下界，全集中存在的比子集中所有元素都大/小的元素集合

上确界和下确界，最小的上界和最大的下界

info

最大最小元一般看端点，如下图：

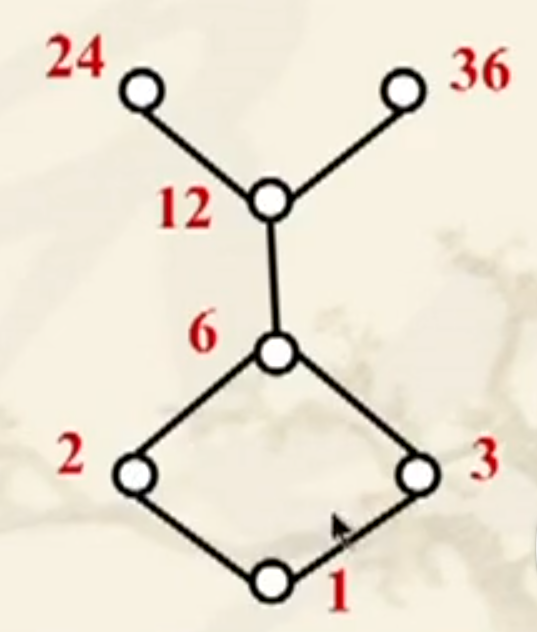
在子集 {2,3,6}\{2,3,6\} 中就没有最小值，因为 2 和 3 之间不存在偏序关系。

由此可见，若有最值则一定唯一。

该子集的下界对应 1，上界对应 6、12、24、36，注意这里是包含 6 的。

上确界为 6，下确界为 1，同样 唯一。

参考

参考