Rethinking Channel Attention and Position Embedding

SEBlock

SEBlock 作为注意力机制在计算机视觉方向的开山鼻祖，为众多通道注意力指引了方向。

传统的通道注意方法致力于构建各种通道重要性权重函数，这种权重函数要求每个通道都有一个标量来进行计算，由于计算开销有限，简单有效的全局平均池化（ $GAP$ ）成为了他们的不二之选。

但是一个潜在的问题是 $GAP$ 是否能够捕获丰富的输入信息，也就是说，仅仅平均值是否足够表示通道注意力中的各个通道。

因此有以下分析：

不同的通道可能拥有相同的平均值，而其代表的语义信息是不相同的；
从频率分析的角度，可以证明 $GAP$ 等价于 $DCT$ 的最低频率，仅仅使用 $GAP$ 相当于丢弃了其他许多包含着通道特征的信息；
$CBAM$ 还表示，仅使用 $GAP$ 是不够的，因此额外引入了 $GMP$ 。

离散余弦变换

DCT 主要用于数据或图像的压缩，能够将空间域的信号转换到频域上，具有良好的去相关性的性能。二维的 $DTC$ 公式如下（略去了前面的系数）：

f_{h,w}^{2d}=\sum_{i=0}^{H-1}\sum_{j=0}^{W-1}x_{i,j}^{2d}cos(\frac{\pi h}{H}(i+\frac12))cos(\frac{\pi w}{W}(j+\frac12))\tag1

二维的逆 $DTC$ 公式如下：

x_{h,w}^{2d}=\sum_{h=0}^{H-1}\sum_{w=0}^{W-1}f_{i,j}^{2d}cos(\frac{\pi h}{H}(i+\frac12))cos(\frac{\pi h}{w}(j+\frac12))\tag2

我们称二者共有项的基函数：

B_{h,w}^{i,j}=cos(\frac{\pi h}{H}(i+\frac12))cos(\frac{\pi w}{W}(j+\frac12))

这其实是一种加权的形式，我们可以将某些基函数可视化：

上图代表了其值的分布，红色表示接近 $1$ ，蓝色表示接近 $-1$ ，绿色表示接近 $0$

可以看出其是十分有规律性的，因为基函数是位置相关的，对于不同的 h,w，其拥有不同的权重，这可以看作一种位置嵌入。

下面证明 $GAP$ 是二维 $DCT$ 的特例，令 $h,w$ 都为 $0$ ：

\begin{align} f_{0,0}^{2d} &=\sum_{i=0}^{H-1}\sum_{j=0}^{W-1}x_{i,j}^{2d}cos(\frac{\textcolor{red}{0}}{H}(i+\frac12))cos(\frac{\textcolor{red}{0}}{W}(j+\frac12))\\ &=\sum_{i=0}^{H-1}\sum_{j=0}^{W-1}x^{2d}_{i,j}\\ &=gap(x^{2d})HW \end{align}

这代表着二维 $DCT$ 变换的最低频率分量，因此 $SENet$ 可以表示为：

根据公式 $(2)$ 我们可以知道特征可以被分解为不同频率分量的组合，自然而然地，可以将其在通道注意力上进行推广——使用多个频率分量。

位置嵌入

位置嵌入最初应该是来自 NLP，最近在计算机视觉领域得到了广泛的应用。

位置嵌入使得网络能够获取其位置信息，从而提高性能。

位置嵌入在通道注意力中的应用有 Coordinate Attention for Efficient Mobile Network Design

疑问

对 FCANet 存在两点疑问

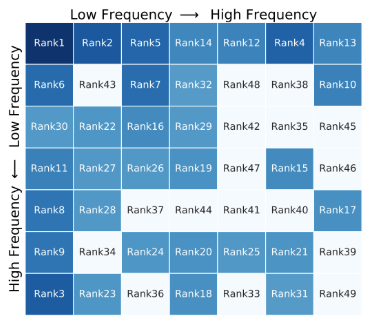
第一，其指出 SENet 中的 GAP 没有利用到频域上的所有信息——即利用 DCT 得到的不同频率分量；然而 FCANet 同样存在的一个问题是，其不是对整个通道使用同一个频率分量，如下图所示：

表示不同信息的不同通道分组使用了不同的频率分量，每个通道分组与上述 SENet 相同，仅仅使用了单个频率分量，这似乎会造成更多的信息丢失，然而其性能相较于 SENet 却提升了近 2 点

第二，论文中对使用仅单个频率分量进行了实验

可以看到，是 GAP 的效果最好；在所有通道都是用 GAP 的效果最好的情况下，对表示部分信息的通道

Rethinking

FCANet 为什么 work

通道冗余：

众所周知，卷积神经网络的通道中往往存在着大量的冗余，这也是我们使用通道注意力的原因，SENet 的成功也能从侧面印证这一点；

位置嵌入：

SENet 使用的 GAP 也可以看做一种加权和，其权值全部为 1，表示对特征图上的每一个像素都一视同仁，由第 2 节我们知道，DCT 分解的频率分量也是一种加权和，且其权值与位置有关，这可以理解为一种位置嵌入。这代表着给空间维度上不同位置赋予不同的权值，从而使得模块能更加关注被选择的部分；

上图为 FCANet 所选择频率分量的基函数的可视化结果，其将每个图分为竖直或者水平的不同几块，显然，这样进行**加权 **是不合理的，这也解释了为什么论文中进行单个频率分量实验效果都没有 GAP 好的原因；

那么 FCANet 为什么会起作用呢？

当通道冗余和位置嵌入结合起来，或许能够一定程度上解释 FCANet work 的原因

通道冗余代表着通道上分布着很多重复的信息，这可能就是 FCA 进行通道分组且仅仅使用单个频率分量但是性能并没有下降的原因；

不同的通道分组会被赋予不同的频率分量，如上图所示，可能是这些分组间的不同权重恰好达到了一种互补的效果，比如第三行的第一张和第四张图、第二行的第一张和第四行的第一张。

上图为论文中进行单个频率分量的实验结果。可以注意到，中间这类“混乱”的权重效果并不好，这可能也从侧面说明，模型拟合复杂关系并没有模拟拟合简单关系的能力强。

除了使模块更易学习，通道分组还为特征编码提供了唯一性的保障，即使出现相似编码的情况降低……

也就是说，FCA 更好的利用了通道中冗余的信息……

如何通过实验证明

根据上述分析，FCA 实际上基于两个假设：

通道间存在大量冗余
位置嵌入在不同冗余的通道内形成互补

对于第一个假设，可以通过减少输入的通道数，来比较 FCA 和 SE 或是原模型的性能，当减小到一定程度时，通道间的信息不再大量冗余，FCA 对通道进行分组会造成一定的信息丢失，性能自然也就不如 SE 或是原模型；

对于第二个假设，可以使用看起来不互补的权重或是看起来互补的权重来进行实验，不过结果可能不能说明什么，因为实际的互补不一定是两两互补，可能在不同通道分组在形成的综合关系中互补

如何改进

不再使用论文提供的频率分量分组方法，可以考虑使用两两互补的方法选择权重矩阵，来简化其关系
自行设计位置嵌入的函数（可选）
在通道数大的地方使用该模块，通道数小的地方去除，或者是使用小的通道分组数，可能会因为信息丢失而造成精度损失

SEBlock​

离散余弦变换​

位置嵌入​

疑问​

Rethinking​

FCANet 为什么 work​

如何通过实验证明​

如何改进​